Supermodels: A guide to public
policy
This paper has its origins in work I have done for the Australian Consumers' Association over the last twelve months. The views and conclusions are mine, but much of the inspiration and information has come from the ACA. I would like particularly to acknowledge the contributions of Louise Sylvan and Catherine Wolthuizen from the ACA, and Dr Hazel Bateman from the University of New South Wales. The book Forced Saving, which Hazel has written in collaboration with Geoffrey Kingston and John Piggott, is a superb compendium of information and analysis of superannuation policies and practices; it has been of great assistance in this research. The ACA has a strong interest in financial issues, an interest that has been growing as financial services account for an increasing portion of the household budget. On average, Australian households spend around $3600 a year (7 percent of total household expenditure), on financial and insurance services. That's more than we spend on operating motor vehicles or on buying furniture and whitegoods.(1) And that doesn't include financial payments passed through the business sector, such as credit card interchange fees. Although specialist academic researchers have been working on superannuation for some time (Hazel Bateman and John Piggott wrote a comprehensive study for EPAC in 1993), it is only recently that it has become a regular issue in the financial press and, increasingly, in the popular media.
That bumper performance is not likely to be repeated in the foreseeable future. The 1990s were unusual in three respects. The first was a steady fall in long-term bond rates as fears of inflation subsided. Such falls are rare; the previous sustained fall in bond rates was between 1920 and 1930. The second was a large number of privatizations and de-mutualizations, often pitched, politically, at low prices, which resulted in high capital gains after listing. (The political gain from undervaluing privatization share issues more than offsets the political odium from stripping public assets.) The third was the tremendous boost in funds coming into capital markets from the superannuation industry itself - not only in Australia, but also in other developed countries. Few industries have such an opportunity to create the conditions for their own success, but in time even the optimists on Wall Street come to understand that price/earnings ratios of 30:1 or 50:1 are unsustainable. The period of financial exuberance has ended. Corporate collapses and lower investment yields have wiped away the optimism of the 1990s. The outlook for the medium term, perhaps the long term, is much more subdued, and people are going to scrutinize their policies more carefully. When industry-wide returns are in the order of 10 or 12 percent a plus or minus two percent return is neither here nor there; when they are in the order of 4 to 6 percent such variations become important to investors. The ACA isn't in the business of financial advice; neither am I. But, as with any complex consumer product, particularly one we have to buy, it is necessary to understand what was and wasn't important in influencing the performance of superannuation. Contribution rates, taxes, fees, earnings? One way of answering these questions would have been a conventional journal search, supplemented perhaps by our own resources. But the situation is too dynamic to allow for reliance on published studies. If, say, we wanted to find the results of a five percent decrease in contribution tax, we needed some way to provide rapid answers. Would a five percent decrease in earning tax compensate for a five percent decrease in contribution tax? Applied policy research requires us to be able to answer "what if" type questions. The most cost-effective way is through modelling. There are two approaches to modelling - one comprehensive, the other simplified. A short historical diversion may describe the difference and the uses of the two types. In the lead up to the 1973 OPEC oil price hikes and embargoes Royal Dutch Shell was the only company to anticipate what was happening. They invested in oil inventories and sold soon-to-be excess tanker capacity to their competitors. All the companies, including Shell, had planning and forecasting departments, staffed by specialist analysts who had developed sophisticated models on mainframe computers. Shell, however, also had an analyst called Pierre Wack, who developed a simplified model of world oil supply, demand and price - a model which he proudly claimed had no equation more complex than a linear function of the nature Y = Ax + B. His model was easily manipulable by hand calculator (spreadsheets were still ten years off), and, most important, its workings were transparent. In its simplification it had lost precision, but it was credible because it was transparent. It helped board members and other stakeholders learn about the workings of the world's oil markets. For these reasons Wack had a much easier time convincing the company's board than those who came from the central planning and forecasting departments in Shell and other companies.(3) Comprehensive models have their place. They are particularly useful for detailed planning in systems which can be described with a set of endogenous, controllable variables within known and previously experienced ranges. They are often less suited, however, to answer "what if" type questions of the sort the policy analyst might wish to ask. In such cases we are better served by simple models. Edith Stokey and Richard Zeckhauser of the Kennedy School of Government, Harvard University, describe the purpose of simplified modelling:
Paul Loomba, Professor of Management at Baruch College New York, also stresses the need for reductionist models.
The process of developing and refining a model of superannuation has allowed us to understand the key policy issues in superannuation - in particular the influence of fees and charges. I named our modest spreadsheet "supermodel.xls". It is developed in Excel, and is available on this link. It's in three parts - an input zone, a set of workings, and an output zone. The set of workings contains simple difference equations - the only complication being some Boolean equations to prevent it from delivering results prohibited by legislation (e.g. fees greater than the account balance.) The model is available in a more user-friendly form, at the ACA website, (http://www.choice.com.au - follow the links to superannuation) but that version doesn't show the model's workings. The model's input zone is shown below. Every variable in the right hand column can be manipulated by the user:
Our representative worker (let's assign an androgynous name like Chris), with default conditions as shown on the screen above, does reasonably well on a modest lifetime salary. Chris accumulates $385 000, which, in a 20 year annuity, should give a retirement income around the same as working salary. (Calculation of the annuity value, a crucial issue in adequacy, is covered in the next section.) Chris, although on a modest average salary ($32 500, a little below average weekly earnings(8)) is idealized, but it's useful to start with an idealized starting point. Chris has starts work at the age of 20, and has 45 years of unbroken full time work. For a model of this nature it would be too onerous to go through all sensitivities. (The model is infinitely variable.) In general, the model shows the high compounding effect of early contributions, and the benefits of preservation - leaving funds to earn income later in life when contributions have accumulated. Preservation Chris can retire earlier than 65, and choose whether or not to preserve. The effect is strong.
(The reason there is only a small fall in preserved accumulation with earlier retirement is that the salary gradient assumption sets the finishing salary at $40 000 at the retirement age, which means higher contributions at an earlier age if retirement is earlier.) Even if Chris retires early, if there is a buffer of saving or a lump sum such as an inheritance or termination payment, there is a significant benefit in preservation. Superannuation funds accumulate strongly in the last few years because of growth from a high base. Early retirement In order to remove the income gradient effect above, we can model the effect of early retirement with and without preservation but with a flat salary - in this case a flat salary of $29 800 which will give the same lump sum for Chris.
This illustrates the effect of early redundancy or retirement. If Chris can hold on, then the effect of early retirement, in itself, is not as serious as the necessity to make an early call on superannuation.
When one is young, however, retirement is a long way off, and it is probable that young people feel little need to look at the performance of their funds, particularly when balances are low. But, because of the effect of compounding over a long time, good performance in early years is important. Interruption Interruption is most likely to be for raising children, and this is most likely to be in one's mid to late twenties. (The median age of women having babies has risen from 26.3 years in 1978 to 29.5 years in 1998.(9))
Contribution rate and contribution tax The effects of varying contributions and contribution taxes are straightforward and linear. An increase in the contribution rate to 10 percent raises the final accumulation to $428 000, or 11 percent. (A rise to 15 percent, as canvassed by various parties, would raise it to $642 000.) Similarly, reducing the contribution tax to zero would raise the final accumulation to $453 000, or 18 percent (the reciprocal of 0.85). Earning rate This is the most sensitive variable to judge. Because the model does not take account of inflation, a real rate should be used. But what is a reasonable real rate for a long-term investment? A reasonable indication of the market's estimate for a risk-free investment is to take the long-term bond rate which is currently 6.10 percent(10), and subtract an estimate for inflation, which, according to Treasury, should be within a target band of 2 - 3 percent.(11) Taking the mid point of that range gives a real risk-free rate of 3.6 percent. That provides an estimate for a floor rate of return.
The Government Actuary, adviser to the Commonwealth Superannuation Scheme, uses an assumed real return of 3.5 percent.(12) This is even lower than the rate inferred from the long-term bond rate, and must be considered a conservative estimate. In the model we have used a real return of 6.0 percent - a compromise between the high returns of the nineties and the recent low returns.
Fees There are many ways of expressing fees, but the most common is as a percentage of capital. Such a frame gives small figures, but the effect of the levels of fees is significant.
There is a vigorous debate on the measurement of fee levels. In late 2001 Dr Hazel Bateman published a paper on disclosure of superannuation fees(13). One figure in that paper, which showed that the average level of fees and charges was 1.7 percent of assets, captured a great deal of attention. It provoked a rejoinder from the Association of Superannuation Funds of Australia (ASFA) claiming that average fees were only 1.3 percent of assets.(14) The debate was also raised in the letters and columns of the financial press. Averages mean little, for the superannuation industry is far from homogeneous, with a large variety of fee levels. Industry, corporate and public sector funds tend to have low fee levels. Retail funds, on the other hand, tend to have high fee levels, and these (apart from the "small funds") are the fastest growing sector of the industry, as is shown in Table 7.
The main policy issues to have emerged from the fall in returns and the rising use of high fee levels relate to adequacy and equity. If superannuation returns had continued at the rate of the 1990s adequacy would hardly have been an issue, and no one would have noticed the level of fees. The starting point for adequacy is the amount needed to sustain an annuity. This is given by the rather forbidding annuity formula, giving the annuity value A of a lump sum S, spread over n years, with a return of r.
If n is set at 20 years (from retirement at 65 to age 85), and S is set at $100 000, then the relation between A and r, that is, the amount of income each $100 000 can purchase, is given in Table 9 below.
What then, does this say about policy? Coming back to our model, Chris will do fairly well if he or she has 40 years of continuous employment - a retirement income of $28 000, or 87 percent of average lifetime earnings. If Chris retires at 60 and preserves, the penalty is slight provided Chris can hold off dipping into superannuation for five years.
Failure to preserve has drastic results, both in terms of the value of the accumulation and the need to stretch out the annuity over more years. Even if Chris takes out an annuity and doesn't try to spend down his or her super, supplementary income support from a pension will probably still be required. A related sensitivity is the variability in management fees and returns - now a more realistic scenario with choice of schemes coming available. Taking a +/- 1.0 percent of return over the life of the policy, and a +/- 0.5 management fee, while holding the twenty year annuity return constant at 4 percent, gives the following range:
In this analysis we have not tried to model basic changes in Chris's situation - long periods of unemployment, periods of casual employment or self-employment, variations in income, high or low levels of salary sacrifice. The point is that if such chance events as early retirement and variations in fund expenses and performance can have such profound effects, then a fortiori, there will be very large variations in adequacy of superannuation schemes. Neighbours with similar earnings over their working lives will find gross differences in their retirement fortunes. One's lifetime earnings will not be a guide to one's retirement income. Gross estimates of adequacy of the superannuation scheme, such as those published in the Treasurer's Intergenerational Report, overlook the range of outcomes of superannuation. And while there is a great deal of discussion about the impact of superannuation taxes, the consequences of different rates are minor compared with the consequences of differences in fund performance and fee levels. For Chris, abolition of the contribution tax would be wiped out by a movement in the management fee from 1.0 to 1.6 percent. Blanket moves to raise the superannuation levy would certainly provide more retirement income, but they would also amplify inequities. The other issue, which has been subject to little policy consideration, has been the effect on household liquidity. The 1993 Fitzgerald Report suggested that a possible consequence of compulsory superannuation could be a displacement of other savings.(15) That seems to have occurred.
At first sight one may believe that this is inconsequential; one form of saving has been replaced by another. But there are policy consequences, for superannuation is not liquid. It is not available to finance purchases of household assets such as cars, periods out of work and strikes. One possible consequence is that people are more dependent on the financial sector for loans to purchase household durables. Another is that people may feel less secure in their personal lives, less inclined to take the risk of quitting to study or to find alternative work. Recent research, for example, shows that while objective measures of period of job tenure have changed little over the years, Australians feel less secure about their employment.(16) Another aspect of compulsory superannuation is that those who take out mortgages for their houses find themselves borrowing from and lending to the financial sector at the same time. Another more static model (available on the same website), simulates what would happen to a couple if they were able to re-direct what would otherwise be their superannuation payments to an accelerated paying-off of their mortgage. The couple has modest incomes, and a $150 000 mortgage (all assumptions are built into the spreadsheet). Assuming a spread of 2.0 percent between mortgage borrowing rates and superannuation returns, and assuming the couple saves what they gain through early mortgage repayment, they are better off by around $150 000 when they retire. (For a discussion of this model see Louise Sylvan "The Borrower/lender dilemma".(17)) This calculation is illustrative only, but it serves to illustrate that the present system, where people borrow from and lend to the financial sector at the same time, effectively results in a transfer to the financial sector in terms of the spread between lending and borrowing rates and in management fees. Finally, there is the macroeconomic purpose of the superannuation scheme. This is a scheme that has served different purposes at different times. Originally it was part of the Hawke Government's Accord - a deal stitched together in 1996 to give a wage rise without aggravating inflationary pressures. More lately it has come to be seen as a means of boosting national saving and of relieving the pressure on public pensions.(18) Advocates of compulsory superannuation generally assume that saving is a desirable end in its own right, that it should be compulsory, and that it should occur in the household sector. But if the purpose of saving is to provide for an ageing population, then it is just as important to plan for the real resources which will be needed in the future. These include both private and public investments. In the public sphere are physical infrastructure, sustainable ecosystems, cities which can cater to the needs of an older population and real resources in health care. But Australia does not necessarily offer attractive opportunities for private sector investment - as Alan Kohler of the Financial Review puts it "fund managers are simply running out of things to buy".(19) At the same time Australia faces huge deficits in its public wealth - in its surface transport infrastructure, in environmental restoration, and many other projects which, while offering attractive economic returns, are not amenable to private investors because of their public good characteristics.(20) It is possible Australia is suffering a misdirection of savings with an imbalance between public and private sector investment. We need to see superannuation in this wider context; it is important, but it is no more than the financial system which can fund some of our future investment. We still have to consider those real resources and their productivity, in both the public and private spheres. 1. Source: Derived from National Accounts Cat 5206.0 Household Final Consumption Expenditure, brought to 2001 prices using chain price index, and using an estimate 7.38 million households, from ABS Household Expenditure Survey 1998-89 Cat 6535.0, updated by population movement. 2. These are assets per account, according to APRA figures. APRA records show 24 million "members" - more accurately there are 24 million accounts; many people have more than one account. 3. For a description of Wack's work from a first person perspective, see Wack 1984, and from a detached perspective see Kleiner 1996. 4. Stokey and Zeckhauser 1978 Page 28. 5. Loomba 1978 Page 39. 6. APRA Superannuation trends Table 3. 7. Budget Paper # 1, 2002-03, Table E1. 8. AWE in 2000-01 was $653.60, giving an annual earning of $34 000 (ABS Average Weekly Earnings Cat 6302.0) 9. ABS Yearbook 2001. 10. Reserve Bank 10 Year Bond Rate April 2002. 11. Budget Paper # 1, 2002-03, Page 3.32. 12. Commonwealth Superannuation Scheme Annual Report 200-01 Page 19. 13. Bateman 2001. 14. Clare 2001. 15. Fitzgerald 1993. 16. Norris and McLean 2000. 17. Sylvan 2002. 18. Intergenerational Report 2002. 19. Kohler 2002. 20. Institution of Engineers 2001. Website of the Australian Prudential Regulation Authority at www.apra.gov.au Website of the Association of Superannuation Funds of Australia at www.superannuation.asn.au Hazel Bateman, Geoffrey Kingston and John Piggott Forced Saving - Mandating Private Retirement Incomes (Cambridge University Press 2001). Hazel Bateman "Disclosure of Superannuation Fees and Charges" Paper prepared for the Australian Institution of Superannuation Trustees August 2001. Hazel Bateman and John Piggott "Australia's Mandated Private Retirement Income Scheme: An Economic Perspective" Economic Planning Advisory Council Retirement Income Perspectives: Two papers prepared for the Office of EPAC (AGPS July 1993). The Institutions of Engineers Australia 2001 Australian Infrastructure Report Card (http://www.infrastructurereportcard.org.au). - Public infrastructure - justified and effective 2001 (http://www.ie.org.au) Ross Clare "Are Administration and investment costs in the Australian superannuation industry too high?" (ASFA Research Centre 2001). Vince W Fitzgerald National Saving: A Report to the Treasurer (Fitzgerald Report) (AGPS 1993). Intergenerational Report Budget Paper No 5, 2002. Art Kleiner The Age of Heretics: heroes, outlaws, and the forerunners of corporate change (Doubleday NY 1996). Alan Kohler "Trusts' feeding frenzy as companies abandon super" and "Super heads offshore" Australian Financial Review 22, 23 May 2002. John M Legge "Super - for Some" Dissent Summer 2001/2002. N Paul Loomba Management - A Quantitative Perspective (Collier Macmillan NY 1978) Ian McAuley "Superannuation and the Public Purpose" Dissent Summer 2001/2002. - "FAQ Superannuation" Consuming Interest No 91 Autumn 2002. Keith Norris and Ben McLean "How long do jobs last in Australia?" Australian Bulletin of Labour Vol 26 No 2 June 2000. Senate Select Committee on Superannuation Super Charges: An Issues Paper on Fees, Commissions, Charges and Disclosure in the Superannuation Industry (Parliament House, 1992) Edith Stokey and Richard Zeckhauser A Primer for Policy Analysis (WW Norton NY 1978). Louise Sylvan "Superannuation - Brilliant System or Consumer Rip-off?" Dissent Summer 2001/2002. - "The borrower/lender dilemma" Consuming Interest No 91 Autumn 2002. Pierre Wack Scenarios: The Gentle Art of Re-perceiving (Harvard Business School, Division of Research, ref 9-9785-042 1984, rev 1985). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
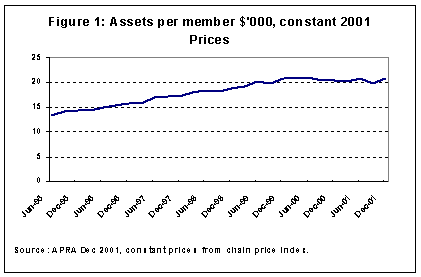 There are two reasons for heightened
community interest. First, superannuation balances have been rising as accounts accumulate
over time and as the compulsory contribution rates have risen. The average balance in a
superannuation account is now around $20 000. That's not a great amount, but it's
enough to arouse some level of interest.
There are two reasons for heightened
community interest. First, superannuation balances have been rising as accounts accumulate
over time and as the compulsory contribution rates have risen. The average balance in a
superannuation account is now around $20 000. That's not a great amount, but it's
enough to arouse some level of interest.

